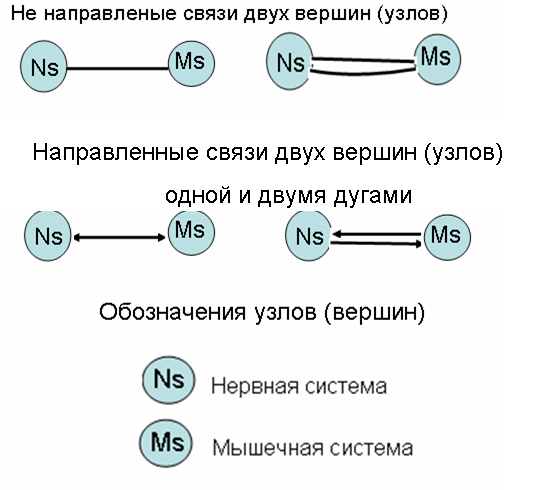
Узловая связь имеет направленные и ненаправленные (дуги).

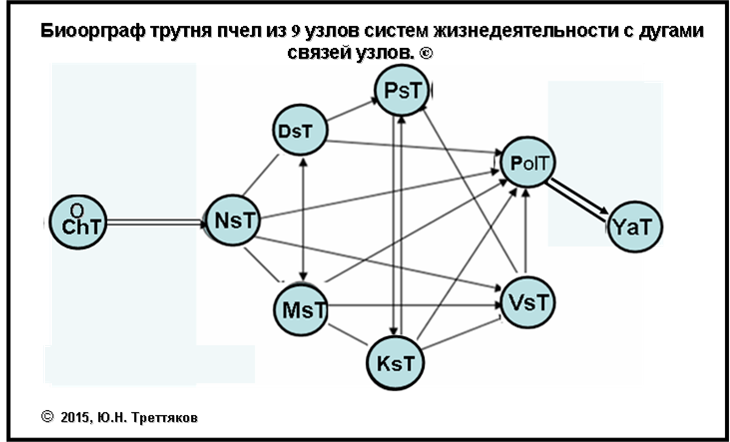
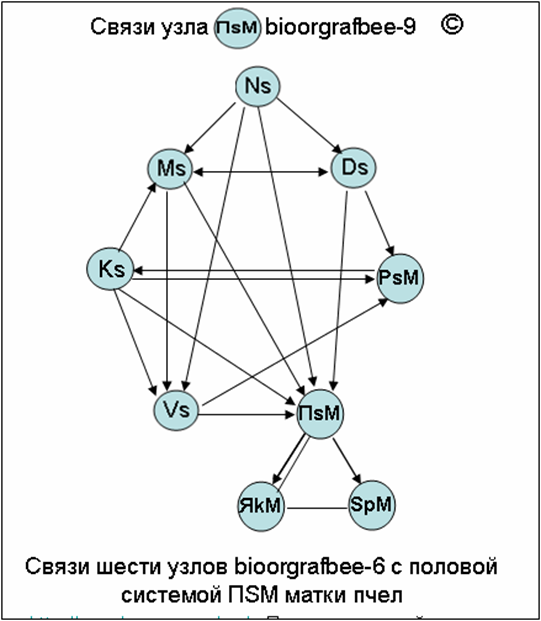
Биологические ориентированные графы (биоорграф) медоносной лчелы.

Исслдование узловых системных связей пчелы

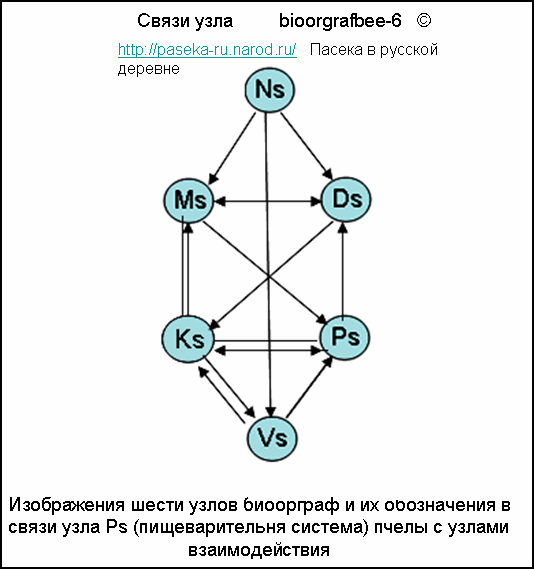
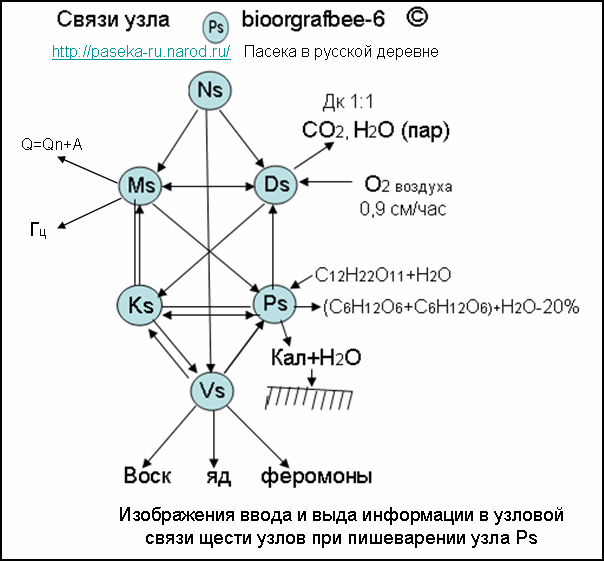
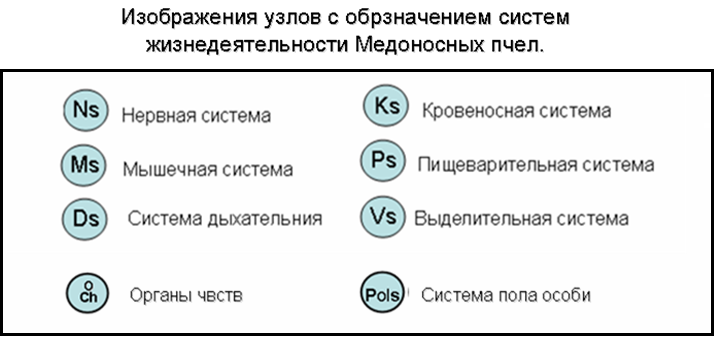
< center>
img src="/pic/bioorgrafbee-8.png"width="507" height="619" border="0" alt=" Биограф пчел-8">

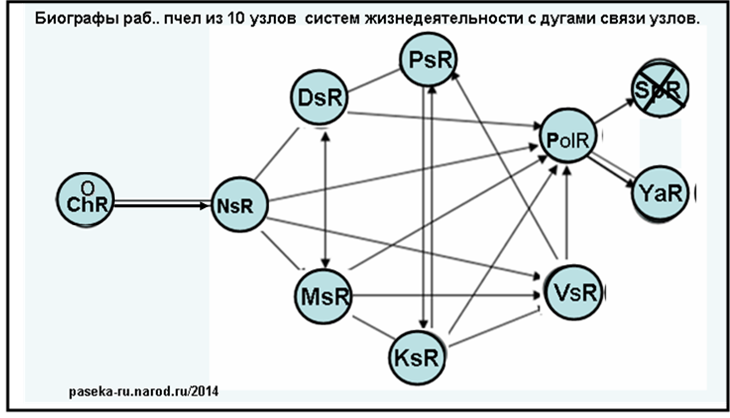
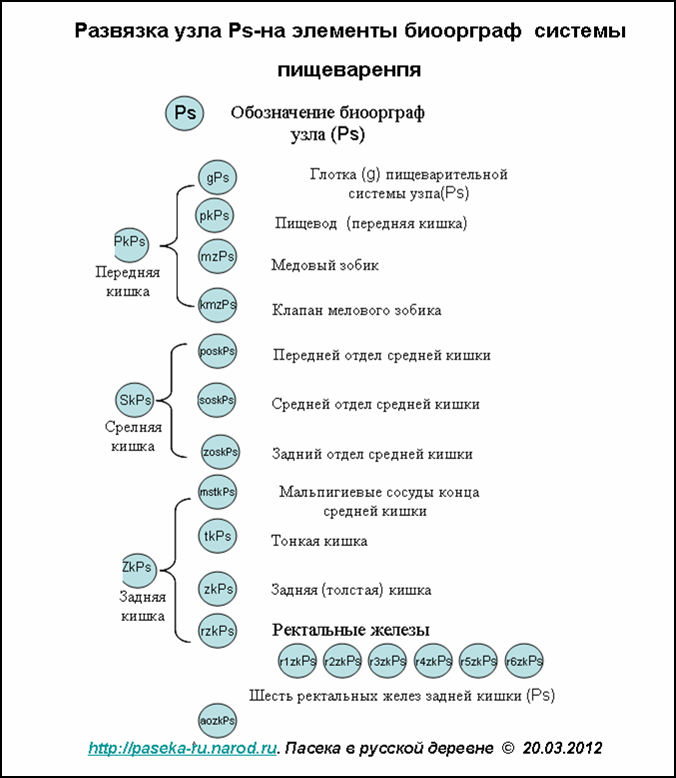
Развязка узлов систем рабочей пчелы

Биологические ориентированные графы (биоорграф) в развязке общего узла графа (Ps) пищеварительной системы медоносной лчелы

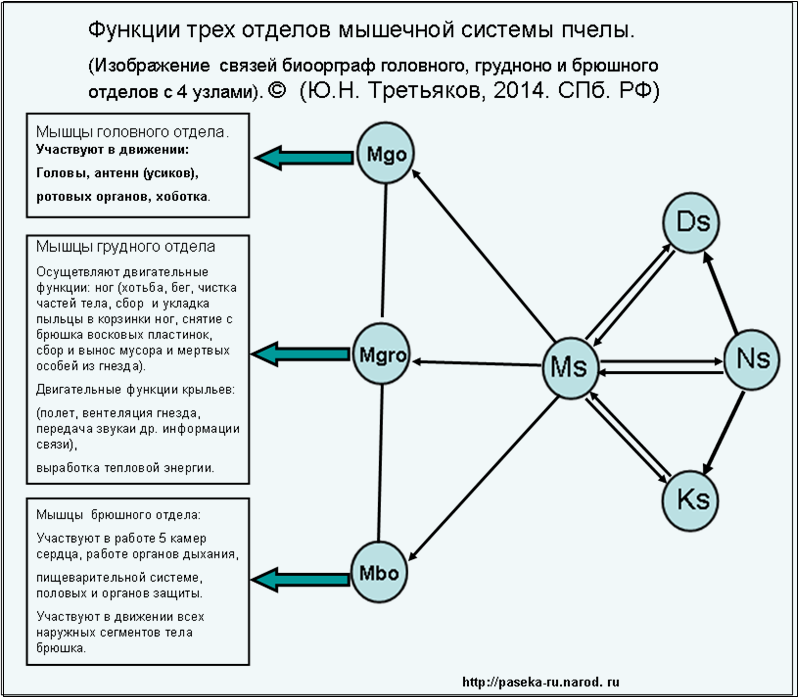
Развязка узла мышечной системы биоорграф по трем отделам тела пчел.©

Статья №1. 14.02.2011

1. Графы.      Графы, Орграфы, Графы связи  связи и биоорграфы в моделировании  с модулями и моделями особей пчел

1.1.  Теория графов

Краткое представление о теории графоф из Википедии

Материал из Википедии — свободной энциклопедии.   /Интернет/

    Тео́рия гра́фов — раздел дискретной математике, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами. В строгом определении графом называется такая пара множеств G=(V,E), где V есть подмножество любого счётного множества, а E — подмножество V×V.

Изображение Графов с шестью вершинами (узлами) и семью рёбрами

(Все изображения смотреть в материалах из Википедии — свободной энциклопедии).   /Интернет/

     При изображении графов чаще всего используется следующая система обозначений: каждой вершине сопоставляется точка на плоскости, и если между вершинами существует ребро, то соответствующие точки соединяются отрезком. В случае ориентированного графа отрезки заменяют стрелками.

     Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет. В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.

     Родоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории. Семь мостов Кёнигсберга — один из первых результатов в теории графов, опубликован Эйлером в 1736.

   Теория графов содержит большое количество нерешённых проблем и пока не доказанных гипотез.  К теории графов также относится целый ряд математических проблем, не решенных на сегодняшний день.

1.1.1.   Применение теории графов

     В схемотехнике (топология) межсоединений элементов на печатной плате или микросхеме представляет собой граф или гиперграф) [2].

      В химии (для описания структур, путей сложных реакций[1], правило фаз также может быть интерпретировано как задача теории графов); компьютерная химия — сравнительно молодая область химии, основанная на применении теории графов. Теория графов представляет собой математическую основу хемоинформатики. Теория графов позволяет точно определить число теоретически возможных изомеров у углеводородов и других органических соединений.

Также в других облостях можно смотреть  материал из Википедии — свободной энциклопедии

Также других облостях можно смотреть  материал из Википедии — свободной энциклопедии

1.2.  Ориентированный граф

Материал из Википедии — свободной энциклопедии

1.2.1.  Краткое представление орграф

      Ориентированный граф (кратко орграф) — (мульти) граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках (Оре) и просто рёбрами.Формально, орграф D=(V, E) есть множество E упорядоченных пар вершин .Дуга {u, v} инцидентна вершинам u и v. При этом говорят, что u — начальная вершина дуги, а v — конечная вершина.

Изображение орграфов с тремя узлами

(Все изображения смотреть в материалах из Википедии — свободной энциклопедии).   /Интернет/

     Орграф, полученный из простого графа ориентацией ребер называется направленным. В отличие от последнего, в произвольном простом орграфе две вершины могут соединяться двумя разнонаправленными дугами.

     Ориентированный граф, полученный из заданного сменой направления ребер на противоположное, называется обратным.

Направленный полный граф называется турниром

Связность орграф

Маршрут орграф

     Маршрутом в орграфе называют чередующуюся последовательность вершин и дуг, вида v0{v0,v1}v1{v1,v2}v2...vn (вершины могут повторяться). Длина маршрута — количество дуг в нем. 

Путь орграф

Путь есть маршрут в орграфе без повторяющихся дуг, простой путь — без повторяющихся вершин. Если существует путь из одной вершины в другую, то вторая вершина достижима из первой.

Контур  орграф

Контур есть замкнутый путь.

             Бесконтурный орграф.

Направленный ациклический граф или гамак есть бесконтурный орграф.

      Орграф сильно связный, или просто сильный. если все его вершины взаимно достижимы; односторонне связный, или просто односторонний если для любых двух вершин, по крайней мере одна достижима из другой; слабо связный, или просто слабый, если при игнорировании направления дуг получается связный (мульти)граф;

      Простым орграфом представимы антирефлексивные отношения, в общем случае требуется орграф с петлями. Если отношение симметрично, то его можно представить неориентированным графом, а если антисимметрично, то направленным

1.2.2.  Применение орграфов

    Орграфы широко применяются в программировании как способ описания систем со сложными связями. К примеру, одна из основных структур, используемых при разработке компиляторов и вообще для представления компьютерных программ — граф потоков данных.

o       В комбинаторике перестано́вка — это упорядоченный набор чисел  обычно трактуемый как биекция на множестве , которая числу i ставит соответствие i-й элемент из набора. Число n при этом называется порядком перестановки.

      В теории групп под перестановкой (подстановкой) произвольного множества подразумевается биекция этого множества на себя.\

<